What's a DAG, anyway?

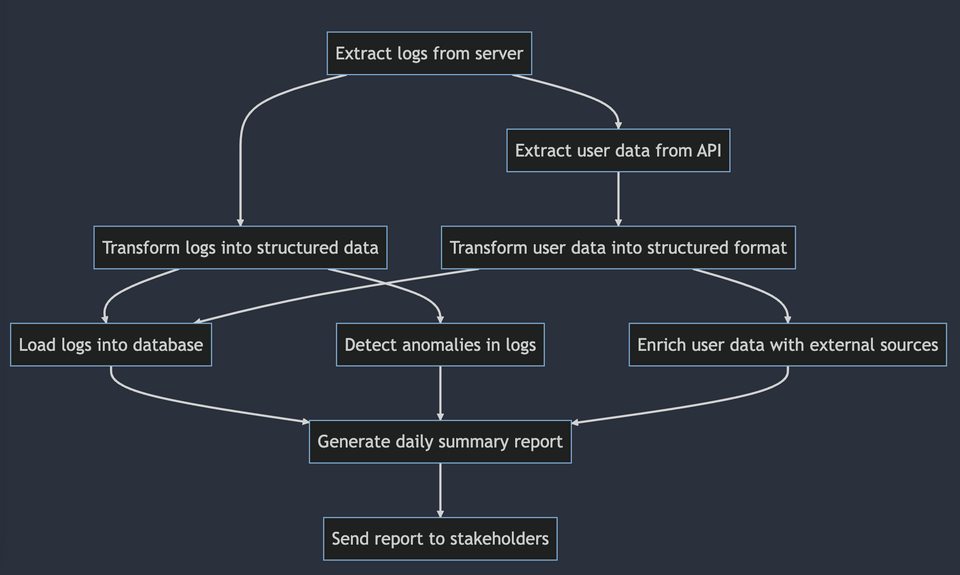
If you are working in Data, you have probably heard the term DAG. You've also probably unwrapped the acronym to learn that it stands for Directed Acyclic Graph and you've probably seen a similar picture to visualize them.

But, have you dived a bit deeper than that? DAGs have lots of fun properties that make them very useful for certain applications, especially in Data Engineering!

Directed acyclic graphs (DAGs) are a type of graph data structure that have a number of mathematical properties that make them particularly well-suited for data flow programming and scheduling tasks that involve dependencies. In this article, we will explore some of these properties in more detail and see how they make DAGs the perfect choice for these types of tasks.

Directed

In a graph, "directed" refers to the fact that the edges in the graph have a specific direction, as opposed to being undirected. This means that each edge in a directed graph is associated with a specific starting vertex (also known as the tail) and a specific ending vertex (also known as the head). For example, in a directed graph that represents a flow of data, the edges might represent the flow of data from one processing stage to another, with the direction of the edge indicating the flow of data.

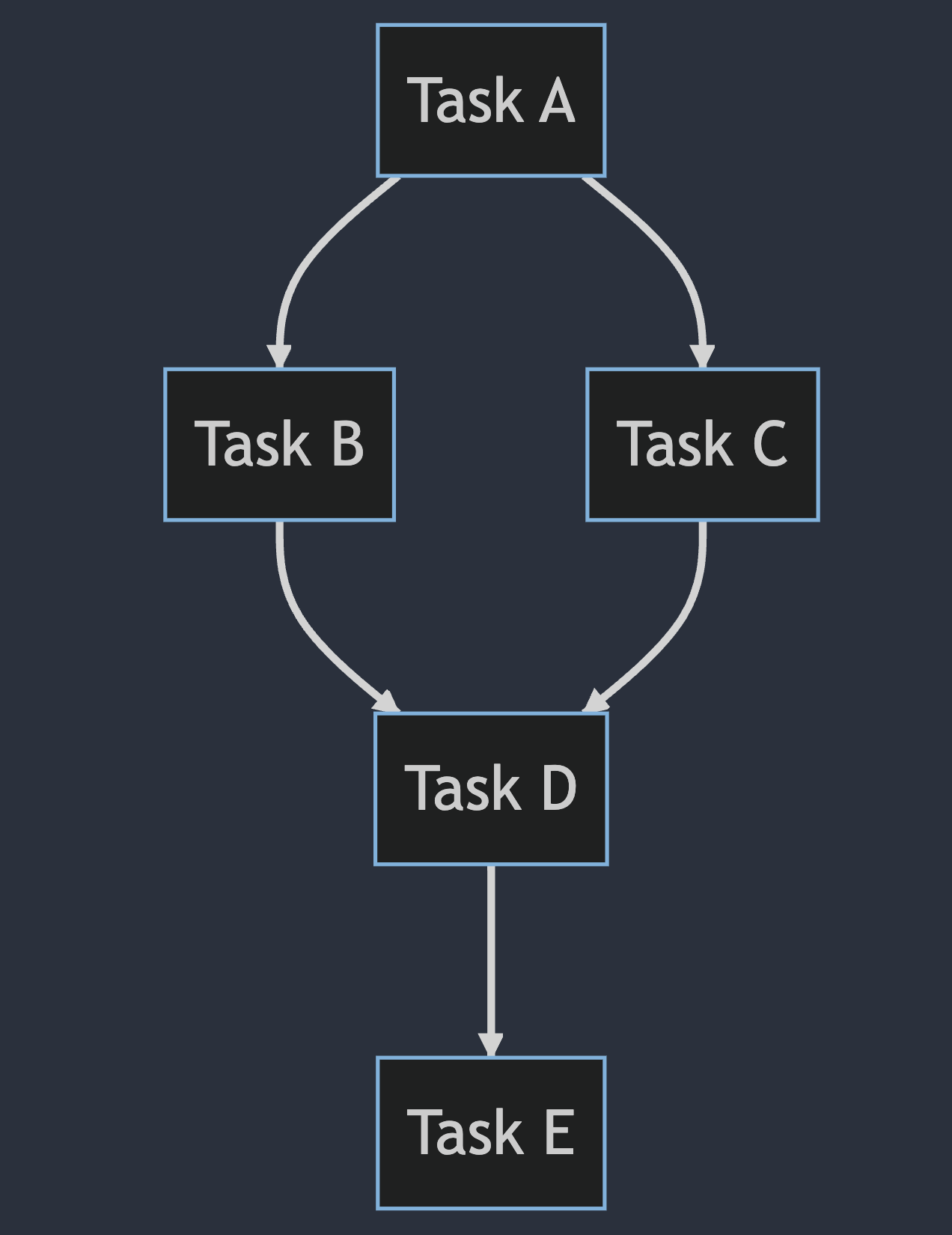
The usefulness of directed graphs lies in the fact that they can represent relationships or dependencies between vertices that are not symmetrical. In an undirected graph, the relationship between two vertices is always mutual, meaning that if there is an edge connecting them, then the relationship goes both ways. In a directed graph, however, the relationship between two vertices can be one-way, meaning that there is an edge connecting them but the relationship does not necessarily go both ways. This is useful because it allows directed graphs to represent relationships that are not mutual, such as when one task depends on another but not vice versa.

This property alone is not really enough to define data pipelines as we could easily run into tasks that depend on each other, which would cause the pipeline to come to a standstill. Luckily, we can introduce a restriction on graphs to exclude these situations.

Acyclic

Another important property of DAGs is that they are acyclic, which means that they do not contain any cycles.

In a graph, a cycle is a path that starts and ends at the same vertex and contains at least one edge. For example, consider the following graph:

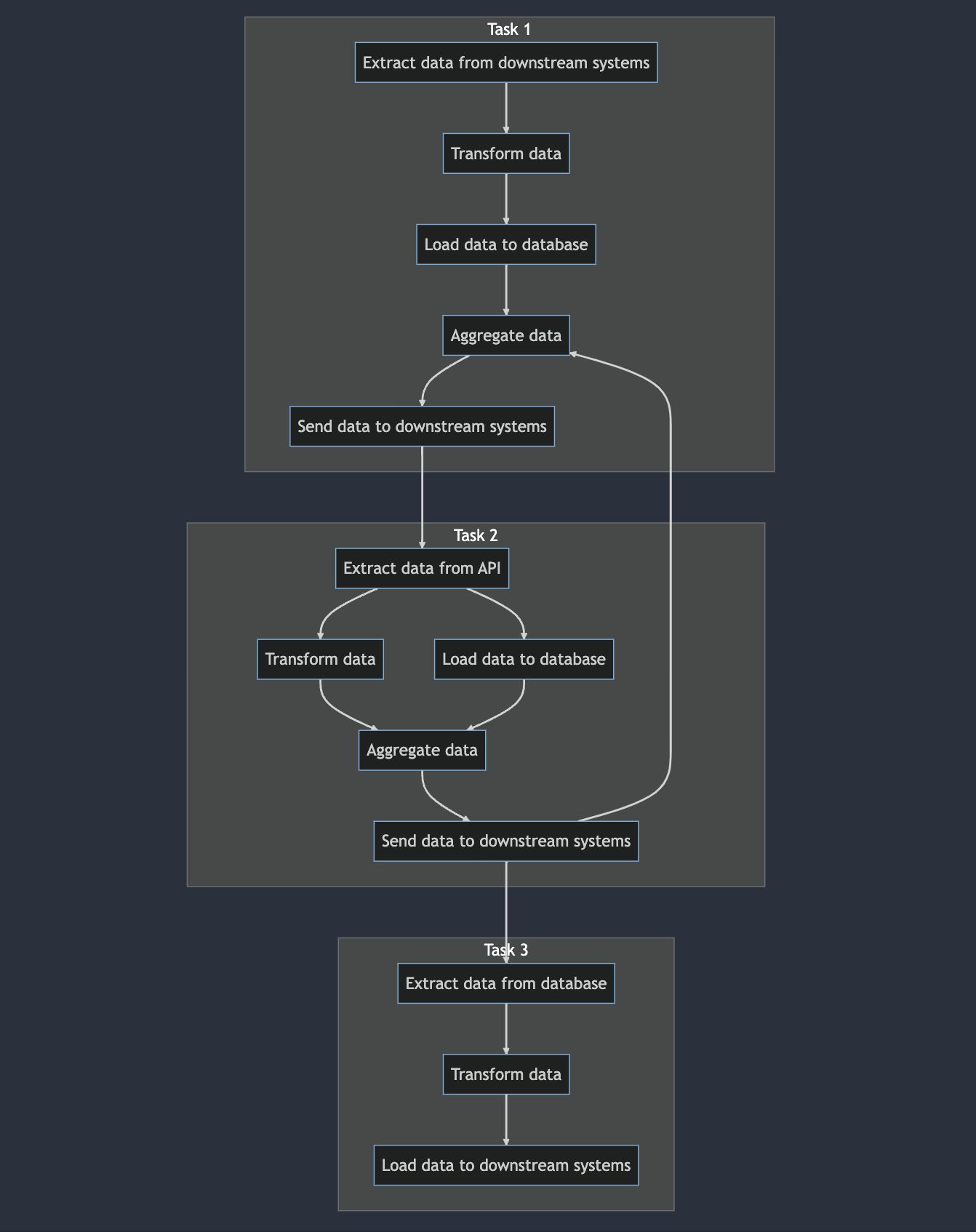
In this graph, there is a cycle that starts at the Aggregate data subtask in Task 1, goes to the end of Task 2, and wraps back around to Aggregate data. This is a cycle because it starts and ends at the same vertex and contains at least one edge.

Cycles can occur in both directed and undirected graphs, and they are typically considered to be undesirable in certain types of graphs because they can cause problems.

Not allowing cycles is significant because it allows DAGs to represent tasks or data flows that cannot have circular dependencies. In other words, if there is a task that depends on another task, it cannot also be a prerequisite for that task. This makes DAGs particularly useful for scheduling tasks, as they can ensure that tasks are executed in the correct order and that no circular dependencies are created.

Relationships

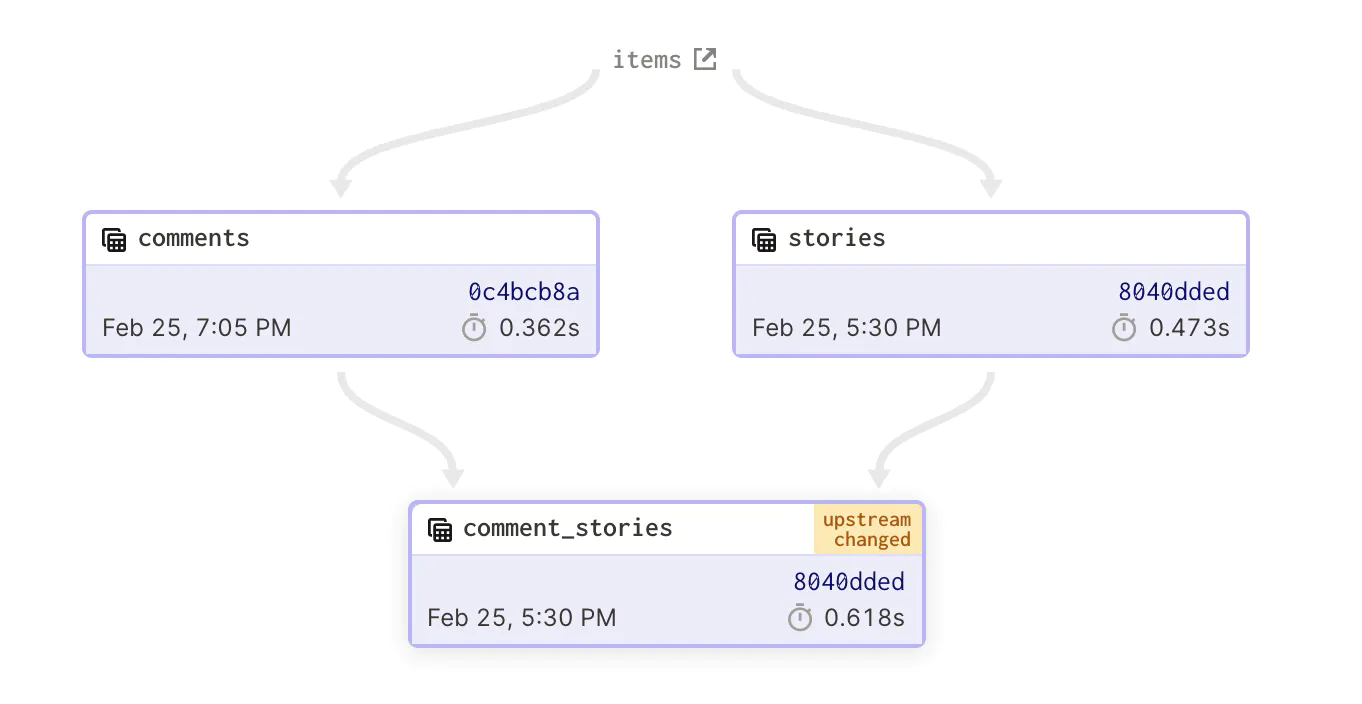
One of the main reasons why DAGs are so useful for data flow programming and scheduling tasks is that they allow for the efficient representation of dependencies. In a DAG, dependencies between tasks or data flows are represented as edges in the graph, with the direction of the edge indicating the direction of the dependency.

For example, if task A depends on task B, the edge in the DAG would go from B to A. This makes it easy to see the relationships between tasks and to understand how they fit together in the overall flow of the program or schedule.

Parallelism

Another important property of DAGs is their ability to represent parallelism. Because DAGs do not contain cycles, it is possible to identify tasks that can be run in parallel with each other. For example, if two tasks have no dependencies on each other, they can be run concurrently, which can greatly improve the efficiency of the program or schedule.

Topological sorting

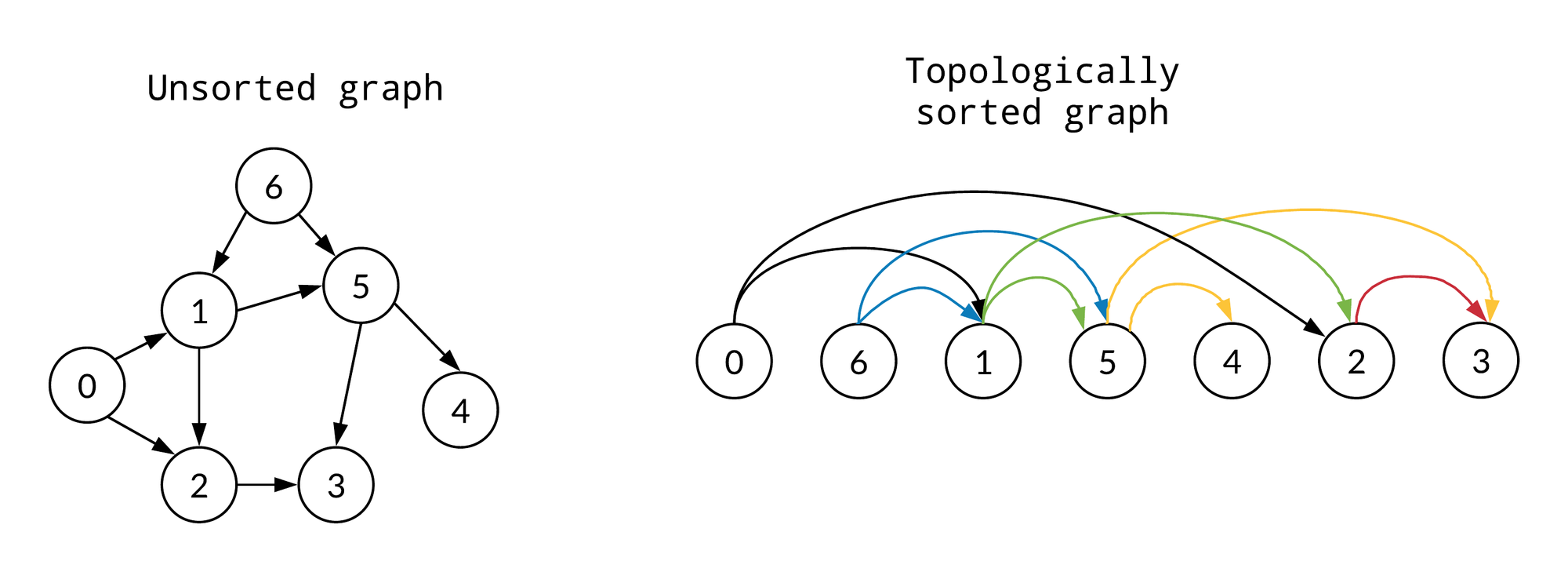
One of the key mathematical concepts that underlie the usefulness of DAGs is the idea of a topological sort. A topological sort is an algorithm that takes a DAG as input and produces a linear ordering of the vertices (or nodes) in the graph such that, for every edge uv from vertex u to vertex v, u comes before v in the ordering. This is significant because it allows for the efficient determination of the order in which tasks or data flows should be executed in a DAG.

There are a number of different algorithms for performing topological sorts, but one of the most well-known is the depth-first search algorithm. This algorithm works by starting at a vertex and following all of the edges emanating from it, recursively visiting all of the vertices that are reachable from it. The vertices are then added to the ordering in the reverse order in which they are finished being visited. This ensures that all dependencies are taken into account and that the resulting ordering is a valid topological sort.

Transitive reduction

Transitive reduction of directed acyclic graphs (DAGs) is the process of removing certain edges from the graph in such a way that the resulting graph is still a DAG and retains the same transitive closure as the original graph, but has the minimum number of edges.

This allows easier reasoning about dependencies in a DAG.

The transitive closure of a graph is a graph that represents all of the reachable vertices from a given vertex. For example, consider the following graph:

A ---> B ---> C
 \         /
  \       /
   ----> D

In this graph, the transitive closure of vertex A would be a graph that includes vertices A, B, C, and D, because these are all reachable from vertex A. The transitive closure of vertex D would be a graph that includes only vertex D because there are no other vertices reachable from D.

Transitive reduction is useful because it allows for the removal of certain edges from the graph that are not strictly necessary, while still preserving all of the reachable vertices. This can be useful in situations where the graph is too large or complex, and reducing the number of edges can make it easier to work with.

There are a number of algorithms that can be used to perform transitive reduction on a DAG, including the Tarjan algorithm and the Gabow algorithm. These algorithms work by identifying edges that can be removed without changing the transitive closure of the graph, and removing them in order to reduce the size of the graph.

Non-Data Engineer use cases?

DAGs are versatile data structure that has a number of applications beyond data engineering. Some of the other areas where DAGs are commonly used include:

1. Scheduling: DAGs are often used to represent schedules or task dependencies in scheduling applications. Because DAGs do not contain cycles and can represent the flow of tasks in a specific order, they are well-suited for this purpose.
2. Compilers: DAGs are used in compiler design to represent the flow of data through various stages of the compilation process, such as lexical analysis, parsing, and code generation.
3. Data mining: DAGs are used in data mining to represent relationships between data items, such as the relationship between a customer and the products they have purchased.
4. Biology: DAGs are used in biology to represent relationships between biological entities, such as genes and proteins.
5. Economics: DAGs are used in economics to represent relationships between economic entities, such as the relationship between companies and their suppliers.
6. Social networks: DAGs are used to represent social networks, with the vertices representing people and the edges representing relationships between people.
7. Computer science: DAGs are used in a wide range of computer science applications, including algorithms, data structures, and computational complexity.

Overall, DAGs are a powerful and flexible data structure that has a wide range of applications in a variety of fields.